Binomio de Newton

Hoy en Matemáticas hemos estado repasando lo que dimos el año pasado, y ha salido lo de las identidades notables [(a+b)2, (a-b)2, (a+b)(a-b)...]. Además, el profesor ha nombrado de pasada algo del Binomio de Newton, la expresión general de (a+b)n.
Más tarde, en Tutoría, yo estaba aburrido como una ostra por las estupideces que estaban diciendo los que se presentaban a delegado de curso (evidentemente, yo no he querido participar. Ya tuve suficiente con lo de hace dos años, cuando me derrocaron). Así que he cogido un papel, y me he puesto a escribir.

Primero, he resuelto (a+b)2. Después, (a+b)3. Así, hasta llegar a (a+b)5. He obtenido los siguientes datos:

  • (a+b)2 = a2+2ab+b2
  • (a+b)3 = a3+3a2b+3ab2+b3
  • (a+b)4 = a4+4a3b+6a2b2+4ab3+b4
  • (a+b)5 = a5+5a4b+10a3b2+10a2b3+5ab4+b5

Luego, he hecho un montón de cálculos extraños que ahora no entiendo ni yo (especialmente porque están distribuidos por dos hojas diferentes, y escritos en diferentes momentos de la clase). Me he dado cuenta de que los términos que van solos están elevados a n, así que lo primero que he hecho ha sido escribir:

(a+b)n = an+an-1b0+an-2b1+ ··· +a1bn-2+a0bn-1+bn
El siguiente problema con el que me he topado han sido los números que faltan. Por ejemplo, con esta fórmula, (a+b)2 sería a2+ab+b2. Por tanto, faltan unos números que multipliquen los términos del polinomio.
Si se ordenan los valores, se obtiene este curioso triángulo:

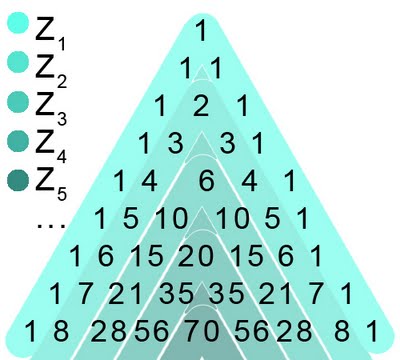Sé que no es estéticamente agradable, pero sólo es ilustrativa. Al paracer, se llama Triángulo de Tartaglia.
Si nos fijamos, cada fila contiene, ordenados, los valores por los que hay que multiplicar cada término del polinomio. Además, cada número es la suma de los dos inmediatamente superiores. He hecho una división por cercanía al borde, y las he nombrado. Así, si nos toca (a+b)3 podemos aplicar la fórmula de antes:

a3+a2b+ab2+b3

y multiplicar cada término por el número correspondiente. Como estamos con el valor de n=3, nos vamos a la tercera fila del triángulo: aparecen los números 1, 3, 3, 1. Multiplicamos, y nos sale

z1a3+z2a2b+z2ab2+z1b3 = a3+3a2b+3ab2+b3

Ahora toca añadir el valor z a la expresión general:

(a+b)n = z1an+z2an-1b0+z3an-2b1+ ··· +z3a1bn-2+z2a0bn-1+z1bn

Si el valor de n es par, en el término central tendríamos zn/2.

Me parece que la fórmula es válida, lo que no tengo claro es si hay algo para saltarse el triángulo como referencia. Y con esto, ya vale de Matemáticas por esta semana.

Tags:

Esta entrada fue publicada el Martes, septiembre 29th, 2009 at 19:00y está archivada como . Puedes seguir los comentarios a esta entrada a través del feed RSS 2.0. Puedes dejar un comentario, o hacer trackback desde tu propio sitio.

2 Responses to “Binomio de Newton”

Leave a Reply