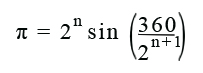Cosas en General

No se integró en la sociedad.

A una semana de la temida Selectividad todo alumno de 2º de Bachillerato que quiera dejar de serlo se empieza a poner nervioso ante la perspectiva de un buen concentrado de exámenes en apenas tres días. Y claro, como en todas las asignaturas entra todo el temario, toca repasar las tres evaluaciones. Lo cual es bastante pesado, pero en algunos casos te da una visión más general de la asignatura.

Hoy, sin ir más lejos, estábamos haciendo en clase de Física unos ejercicios de gravitación, lo típico para preparar el examen, cuando no sé cómo ha surgido el tema de que si las órbitas que describen los cuerpos celestes son elípticas no era lógico que en los problemas supusiésemos que son circulares. Ante eso, el profesor nos ha dicho que, efectivamente, se trata de una elipse, pero que el cálculo de esas trayectorias se eliminó del temario hace tiempo. Una ligera decepción para los que realmente teníamos curiosidad, pero nos ha comentado brevemente el tema y nos hemos quedado satisfechos. Sin embargo, un poco más tarde hemos pasado a la cuestión de los campos eléctricos y, como desde hace unos días ya sabemos integrar, hemos acabado hablando del Teorema de Gauss, que hace unos meses nos saltamos porque, por un lado, aún no sabíamos qué era una integral, y por otro, porque de nuevo es algo que no está en los planes de estudio. Y ni con esas, porque las herramientas matemáticas que son necesarias para trabajar con ese teorema ni siquiera aparecen mencionadas en el temario de 2º.

Contemplar cómo el nivel de asignaturas tan importantes para los futuros científicos o ingenieros como la Física y las Matemáticas no hace más que bajar es desolador. Y si al menos estuviesen ambos niveles compensados, pues no se notaría tanto la diferencia. Pero es que ya desde el curso pasado he necesitado conocimientos sobre cálculo diferencial e integral para poder comprender correctamente ciertos temas, y es bastante inconsecuente que esto se vea en un curso superior cuando hace poco más de 20 años se daba en 3º de BUP (el 1º de Bachillerato actual).

Quiero creer que la formación perdida durante los años de Educación Secundaria se acaba recuperando en la Universidad, pero personalmente preferiría que el puente por el que cruzo el Ebro estuviese diseñado por alguien que tenga una base técnica lo suficientemente sólida. Aunque si la respuesta oficial ante cualquier pregunta que se aleje del temario es “Es que eso no puedo explicároslo”, no sé yo si en unos años no haría mejor construyendo mi propia barca cuando quiera llegar a la otra orilla.

El viernes participé en la primera fase de la XLVIII edición de la Olimpiada Matemática Española. Al igual que el año pasado (cuando quedé 4º, a un par de puntos de clasificarme para la fase nacional), la prueba consistió en 6 problemas a resolver entre dos sesiones de tres horas y media de duración cada una.

La solución al primero, una progresión, era bien sencilla: 20n2. Pero, como siempre, existen dos caminos: el fácil y el difícil. Adivinad cuál elegí yo. Efectivamente, dicha progresión aritmética puede expresarse de forma sencilla (20n2), y de forma compleja, con números combinatorios y demás parafernalia. Pues bien, resulta que, accidentalmente, topé con la expresión compleja, pero no le di mayor utilidad que la de hacerme el interesante. Sin embargo, anteayer ordené los folios de borrador que empleé durante la Olimpiada, y encontré de nuevo la fórmula. La estuve examinando un rato, y me decidí a generalizarla. De ahí pasé a otra ecuación más general todavía, que, tras 38 carillas de sucio y unas 8 horas de quebraderos de cabeza evolucionó hasta la siguiente fórmula:

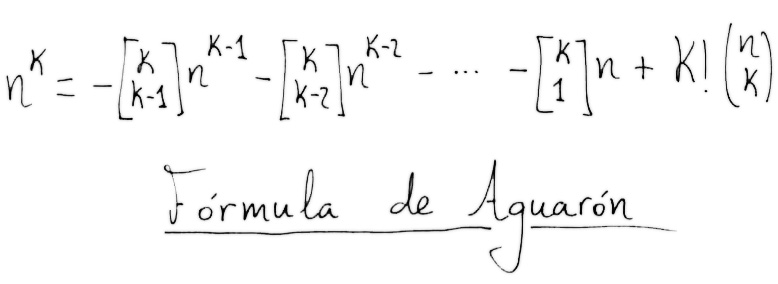
Emplea los números de Stirling, algo que suena muy bien pero que no entiendo

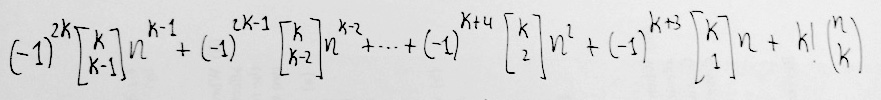
Al no estar esta parte de las Matemáticas estandarizada, he escrito esta otra fórmula que emplea la notación de otros autores

No sé si alguien la habrá encontrado antes, pero la alegría que experimenté al verla terminada no se puede describir con palabras. Quizá sólo con números [inserte risas enlatadas aquí].

En cuanto al resto de problemas, no hubo ninguna anécdota destacable. Tal vez que durante la sesión de la tarde no me encontraba del todo bien, y pasé unas dos últimas horas bastante malas, pero resistiéndome a rendirme aguanté como un Euler hasta el final. Acto seguido, me subí al despacho de Pepe a por un paracetamol; me lo había ganado.

Ésta fue la primera Olimpiada Matemática en la que participaba mi hermano, que aunque va a 4º de la ESO, gracias a un permiso especial de su profesor pudo participar entre los “mayores”. Y, la verdad, no le ha ido nada mal: ayer salieron los resultados, y está en el puesto 36 de la clasificación.

Aunque quisiera, yo no podría deciros el puesto en el que he quedado, ya que al estar ENTRE LOS 8 PRIMEROS no lo sabré hasta el día de la entrega de premios! En efecto, he vuelto a quedar en el top-8, pero hasta el día 13 de enero en el Patio de la Infanta no conoceré el resultado definitivo. No tengo muchas esperanzas, pero siempre cabe la posibilidad de que pueda pasar a la fase nacional…

Si tuviese que definir con un solo adjetivo el curso que estoy acabando, elegiría “tedioso”. A pesar de la supuesta dificultad del Bachillerato (que no es tal; simplemente hay que estudiar a diario y casi ni eso), este último año ha sido de los más aburridos que recuerdo. La verdad es que no hay un único motivo, sino que se debe a varios factores.

Por un lado, el curso está orientado al repaso general de todo lo que se ha visto durante la ESO, lo cual es muy útil para gente que tenga lagunas en sus conocimientos. Pero entonces, ¿qué hacen los que tienen únicamente charcos? ¿Atender a explicaciones que llevamos escuchando desde hace dos años? Quizá al principio sí. Pero cuando llevas más de 5 meses (hablo en términos generales, esto es más marcado en unas asignaturas que en otras) recordando conceptos “olvidados”, el interés se esfuma. Y justo cuando empieza la acción, el curso se acaba.

También cuenta mucho el modo en que se enfoca la asignatura. Pongamos el ejemplo de Matemáticas: una materia que puede resultar apasionante (de acuerdo, quizá para algunos no lo sea, pero la culpa no es suya) se convierte en cuatro horas semanales de ejercicios repetitivos, y ya. Precisamente hoy era la sesión de clausura del Taller de Talento Matemático, y el ponente ha realizado una presentación acerca de la Historia de las Matemáticas: he aprendido más en esos 60 minutos que en dos semanas de clase. Lo admito, es necesario saberse la teoría para poder realizar la práctica, pero el problema es que no hay práctica. Porque, en realidad, los “problemas” que se hacen no son nada problemáticos: son meros ejercicios camuflados. En Geometría quiero sangakus, no calcular chorromil veces lo que mide la sombra de un edificio.

Y esto es ya más personal, pero yo echo de menos la asignatura de Tecnología, una de las pocas en las que se puede tener cierta creatividad. Este curso, estirando mucho, se podría salvar Lengua gracias a los comentarios de texto en los que un servidor puede despotricar un poco más. Pero lo que es cierto es que la creatividad está muy olvidada (aún no la he visto, pero mucha gente me ha recomendado esta charla TED sobre el tema).

Ahora que tengo mi horario encima de la mesa, estoy viendo que en muchas asignaturas pinto poco:

• Inglés: no sé ni por qué voy. Año tras año se dan los mismos tiempos verbales. Realmente, es mi clase de lectura.
• Francés: de entrada, la programación de la asignatura está pensada como un repaso de la ESO. ¿Estudiar? ¡Ja!
• Filosofía: qué se le va a hacer, no me atrae especialmente estar 9 meses aprendiendo memorizando diversas teorías políticas.

Por suerte me queda Dibujo Técnico, mi preferida de este año. No permite una gran expresividad, pero la verdad es que se agradece poder dibujar un rato. Comparado con otras como Filosofía es una auténtica liberación.

En fin, ya queda menos para el verano, y no tanto para 2º de Bachillerato. Parece que promete un poco más: las Mates son más entretenidas, tendré Electrotecnia, Física será sólo Física y no “Física y Química” (aunque, ahora que no me oye nadie, tengo que admitir que le he acabado cogiendo cierto cariño), me quito Francés y Ciencias del Mundo…

Seguiremos informando.

Aparece en “La sonrisa de Pitágoras”, un libro de divulgación matemática que me estoy leyendo estos días.

Se me ha ocurrido una forma de aproximarse a Pi bastante buena, y muy sencilla de entender.

Empecemos con un círculo, simplificado a 4 lados (l). De infinitos lados hemos pasado a 4, no está mal:

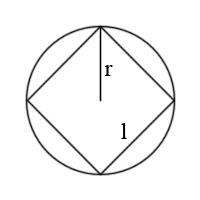
Si tomásemos ese cuadrado como un círculo, su longitud sería 4l. Supongamos que r vale 1 (además, así se simplifican los cálculos), por lo que l valdrá (Teorema de Pitágoras) . Si la fórmula de la longitud es 2(Pi)r, tendríamos que 4=2(Pi), por lo que Pi valdría 2.828…

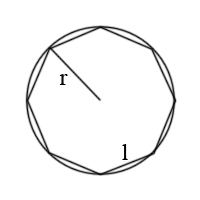
Ahora, tomemos un polígono de mayor número de lados (es más sencillo con los que tengan 2ⁿ lados). En este caso, 8.

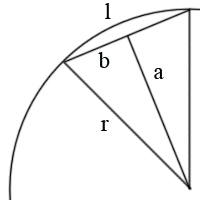
En este caso tenemos un triángulo isósceles cuyos lados iguales son r (1), y el desigual l. Para poder sacar el valor de l tenemos que partirlo por la mitad, de modo que tengamos dos triángulos rectángulos de lados r, a y b.
De este triángulo conocemos la hipotenusa (1), el ángulo recto y el que coincide con el centro de la circunferencia. Como la circunferencia mide 360º (simplificada en 2ⁿ lados, y nosotros tenemos la mitad del triángulo, ese ángulo será 2ⁿ⁺¹. Ahora que conocemos ese ángulo, podemos aplicar la fórmula del seno para hallar el valor de b. En este caso,

sin (360/16)=0.3827…

Como r=1, b=0.3827… Y como l=2b, l=0.7654… Por tanto, la longitud de esta circunferencia será 8l=6.1229…, y Pi tendrá un valor de 3.0615.

De todo esto se saca la siguiente fórmula:

Cuanto mayor sea el valor de n, más dígitos de Pi saldrán. Con n=21 salen 9 decimales. No es gran cosa, pero menos da una piedra.