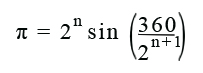Aproximación de Pi
Se me ha ocurrido una forma de aproximarse a Pi bastante buena, y muy sencilla de entender.
Empecemos con un cÃrculo, simplificado a 4 lados (l). De infinitos lados hemos pasado a 4, no está mal:
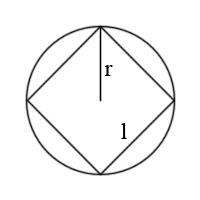
Si tomásemos ese cuadrado como un cÃrculo, su longitud serÃa 4l. Supongamos que r vale 1 (además, asà se simplifican los cálculos), por lo que l valdrá 
(Teorema de Pitágoras) . Si la fórmula de la longitud es 2(Pi)r, tendrÃamos que 4=2(Pi), por lo que Pi valdrÃa 2.828…
(Teorema de Pitágoras) . Si la fórmula de la longitud es 2(Pi)r, tendrÃamos que 4=2(Pi), por lo que Pi valdrÃa 2.828…
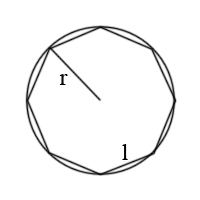
Ahora, tomemos un polÃgono de mayor número de lados (es más sencillo con los que tengan 2n lados). En este caso, 8.
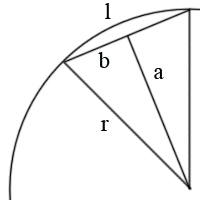
En este caso tenemos un triángulo isósceles cuyos lados iguales son r (1), y el desigual l. Para poder sacar el valor de l tenemos que partirlo por la mitad, de modo que tengamos dos triángulos rectángulos de lados r, a y b.
De este triángulo conocemos la hipotenusa (1), el ángulo recto y el que coincide con el centro de la circunferencia. Como la circunferencia mide 360º (simplificada en 2n lados, y nosotros tenemos la mitad del triángulo, ese ángulo será 2n+1. Ahora que conocemos ese ángulo, podemos aplicar la fórmula del seno para hallar el valor de b. En este caso,
De este triángulo conocemos la hipotenusa (1), el ángulo recto y el que coincide con el centro de la circunferencia. Como la circunferencia mide 360º (simplificada en 2n lados, y nosotros tenemos la mitad del triángulo, ese ángulo será 2n+1. Ahora que conocemos ese ángulo, podemos aplicar la fórmula del seno para hallar el valor de b. En este caso,
sin (360/16)=0.3827…
Como r=1, b=0.3827… Y como l=2b, l=0.7654… Por tanto, la longitud de esta circunferencia será 8l=6.1229…, y Pi tendrá un valor de 3.0615.
De todo esto se saca la siguiente fórmula:
Cuanto mayor sea el valor de n, más dÃgitos de Pi saldrán. Con n=21 salen 9 decimales. No es gran cosa, pero menos da una piedra.