sep
29
2009
Hoy en Matemáticas hemos estado repasando lo que dimos el año pasado, y ha salido lo de las identidades notables [(a+b)2, (a-b)2, (a+b)(a-b)...]. Además, el profesor ha nombrado de pasada algo del Binomio de Newton, la expresión general de (a+b)n.
Más tarde, en Tutoría, yo estaba aburrido como una ostra por las estupideces que estaban diciendo los que se presentaban a delegado de curso (evidentemente, yo no he querido participar. Ya tuve suficiente con lo de hace dos años, cuando me derrocaron). Así que he cogido un papel, y me he puesto a escribir.
Primero, he resuelto (a+b)2. Después, (a+b)3. Así, hasta llegar a (a+b)5. He obtenido los siguientes datos:
- (a+b)2 = a2+2ab+b2
- (a+b)3 = a3+3a2b+3ab2+b3
- (a+b)4 = a4+4a3b+6a2b2+4ab3+b4
- (a+b)5 = a5+5a4b+10a3b2+10a2b3+5ab4+b5
Luego, he hecho un montón de cálculos extraños que ahora no entiendo ni yo (especialmente porque están distribuidos por dos hojas diferentes, y escritos en diferentes momentos de la clase). Me he dado cuenta de que los términos que van solos están elevados a n, así que lo primero que he hecho ha sido escribir:
(a+b)
n = a
n+a
n-1b
0+a
n-2b
1+ ··· +a
1b
n-2+a
0b
n-1+b
n
El siguiente problema con el que me he topado han sido los números que faltan. Por ejemplo, con esta fórmula, (a+b)
2 sería a
2+ab+b
2. Por tanto, faltan unos números que multipliquen los términos del polinomio.
Si se ordenan los valores, se obtiene este curioso triángulo:
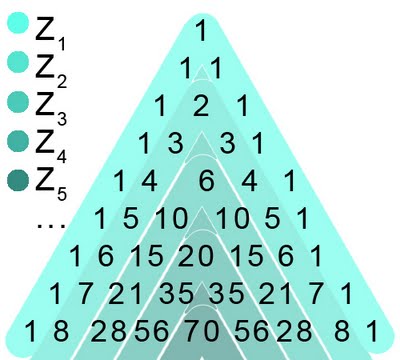Sé que no es estéticamente agradable, pero sólo es ilustrativa. Al paracer, se llama Triángulo de Tartaglia.
Si nos fijamos, cada fila contiene, ordenados, los valores por los que hay que multiplicar cada término del polinomio. Además, cada número es la suma de los dos inmediatamente superiores. He hecho una división por cercanía al borde, y las he nombrado. Así, si nos toca (a+b)3 podemos aplicar la fórmula de antes:
a3+a2b+ab2+b3
y multiplicar cada término por el número correspondiente. Como estamos con el valor de n=3, nos vamos a la tercera fila del triángulo: aparecen los números 1, 3, 3, 1. Multiplicamos, y nos sale
z1a3+z2a2b+z2ab2+z1b3 = a3+3a2b+3ab2+b3
Ahora toca añadir el valor z a la expresión general:
(a+b)
n = z
1a
n+z
2a
n-1b
0+z
3a
n-2b
1+ ··· +z3
a
1b
n-2+z
2a
0b
n-1+z
1b
n
Si el valor de n es par, en el término central tendríamos zn/2.
Me parece que la fórmula es válida, lo que no tengo claro es si hay algo para saltarse el triángulo como referencia. Y con esto, ya vale de Matemáticas por esta semana.
2 comments | tags: matemáticas | posted in matemáticas
may
14
2009
El otro día participé con Ernesto en un concurso de parejas del TTM. Creímos haberlo hecho un poco chapuceramente, pero, contra todo pronóstico, somos los ganadores de 3º de la ESO. En la clasificación general, somos sextos, pero supongo que harán división por cursos.
Jhak también participó, sólo que con uno de 4º. Y puede que también haya ganado (no sabemos si ha quedado 2º o 4º).
Y con esto logramos quedar primeros en los dos concursos que se han hecho este año, el de equipos y el de parejas.
-Soluciones (que no doy)
no comments | tags: matemáticas | posted in matemáticas
may
8
2009
Hoy por la tarde ha sido la undécima sesión del TTM (me parece que la cuarta a la que voy). Hoy no ha habido ninguna charla entretenida, ni presentación de diapositivas, ni papiroflexia. Concurso matemático por parejas. Me he puesto con Ernesto, y hemos ido a la carga.
Bueeeeno… Había 30 problemas. Hemos hecho unos 23. Y hecho bien, unos 14.
No creo que ganemos, pero por lo menos tenemos asegurado el premio del concurso por equipos (que ganamos hace un mes).
No ha estado mal, en cuanto pueda, me acuerde o me lo pidáis pondré los enunciados.
no comments | tags: matemáticas | posted in matemáticas
may
4
2009
Yo siempre he pensado que la letra griega Pi (que nunca pongo porque, misteriosamente, Blogger la anula) está completamente excluida del teclado. ¿Por que no cambian la inútil cedilla (Ç, ç) por Pi?
En teoría, hay una combinación de teclas con la que aparece, pero es algo poco práctico. He pensado que es mejor esto:
Pi = T +T
Tan sólo funciona con algunas tipografías, pero nunca está de más tener un atajo extra.
Arial: TT
Courier: TT
Georgia: TT
Trebuchet: TT
Verdana: TT
Menos da una piedra…
Actualización
Me responden de Microsiervos (se lo envié, como curiosidad), diciéndome algo mucho mejor que mi cutre fórmula:
Pi = &pi = π
no comments | tags: matemáticas | posted in matemáticas
abr
29
2009
Siempre he odiado la fórmula que aparece en los libros del colegio para hallar el volumen del tronco de pirámide:
Vpirámide grande-Vpirámide pequeña
Es fea, y no incita para nada a pensar. Bueno, lo que no incita a pensar son los datos que nos dan: en algunos ejercicios, ya te dicen los volúmenes de las dos pirámides. Así que ayer comencé a cavilar, y hoy he puesto en práctica un método de resolución, que para nada es una fórmula (ya me gustaría).
De modo que a los que, como yo, sólo han oído hablar de la fórmula de arriba les propongo este problema:
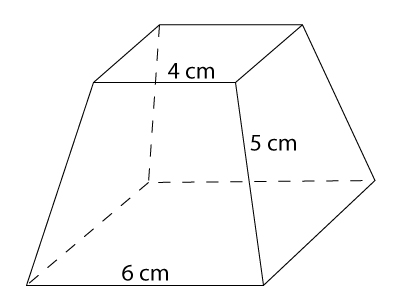
Haya el volumen del siguiente tronco de pirámide:
Mañana, si tengo ganas, pondré la solución (¡con dibujitos de Illustrator!)
no comments | tags: matemáticas | posted in matemáticas
mar
22
2009
Entre varios grupos que acudieron al concurso del otro día del Taller de Talento Mátemático, ganó ¡el nuestro!
(Y eso que, en uno de las respuestas, pusimos “lo sé porque conozco al jardinero”)
no comments | tags: matemáticas, mi vida | posted in matemáticas, mi vida
Sé que no es estéticamente agradable, pero sólo es ilustrativa. Al paracer, se llama Triángulo de Tartaglia.