¡Feliz día de Pi!
¡Felicidades a todos!
Cada dos semanas, aproximadamente, y a lo largo del curso, en el edificio de Matemáticas de la Universidad se hacen unas jornadas dirigidas a chicos de 3º de ESO a 2º de Bachillerato.
Nos enteramos tarde, para la octava sesión, pero por suerte aún quedan bastantes.
La primera “clase” fue el día 20 de febrero, a la que fuimos Alejandro, Alfonso, Álvaro, Ernesto y yo. Trataba sobre el dominó: partidas perfectas y semiperfectas, posibles combinaciones, enunciados que se podían sacar de ello, teoría de grafos… Bastante interesante. Y, para rematar la jornada, estuvo la caída memorable de Álvaro de la silla.
Ayer, viernes 13 (vaya con la friggaatriscaidecafobia) volvimos a la siguiente sesión. Hubo bajas: Alfonso y Álvaro prefirieron quedarse en casa. Ésta vez era una competición matemática por equipos, con problemas sacados del “Rally Matemático sin Fronteras”, una competición originaria de Francia. Es una lástima habernos enterado de este mundillo tan tarde, ya que nos hemos perdido el concurso “Canguro Matemático” y la que acabo de decir. [Interrumpo el sermón: ¿alguien sabe por qué en la calle hay gente tocando la trompeta?]
En fin, nos organizamos por equipos de 6 personas (Alejandro, Ernesto y yo con otros tres de otro colegio), y empezaron a contarnos de qué iba la cosa: eran 8 problemas, extraídos de la edición del Rally de 1996, del nivel de 3º de ESO. Luego, pusieron un nombre a cada grupo: nosotros éramos “Teorema de Fermat” (todos los nombres eran de famosos teoremas).
Nos dividimos en subgrupos (3 parejas), para que cada problema fuese hecho dos veces, y comenzamos con los ejercicios:
1.- Al cociente
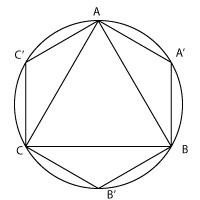
Consideremos los dos cocientes siguientes:
X=Área del triángulo ABC/Área del hexágono regular AA’BB’CC’
Y=Perímetro del triángulo ABC/Perímetro del hexágono AA’BB’CC’
Calculad el valor de X e Y
2.- Llevados por la barca
Tres adultos y tres niños tienen que atravesar un río en una barca tan pequeña que sólo pueden sentarse un adulto o dos niños.
¿Cuál es el número menor de travesías necesarias? (una ida y vuelta tiene dos travesías)
 3.- Banda aparte
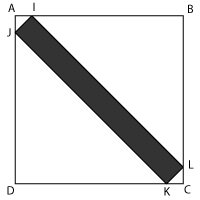
3.- Banda aparte
ABCD es un cuadrado; AI = AJ = CK = CL = 10 cm
El área de la banda rallada es igual a 1 m2
Calculad el valor exacto de lado de este cuadrado.
4.- IVA
En 1995 el tipo del IVA sobre el precio sin impuestos de un artículo pasó del 18’6% al 20’6%.
¿En qué porcentaje ha aumentado el precio final del artículo? (todos los impuestos incluidos)
5.- En helicóptero
El responsable del Rally Matemático Sin Fronteras con residencia en Toulouse ha de ir urgentemente a llevar las pruebas del Rally a Lugo, Barcelona, Andorra y, evidentemente, volver a Toulouse. Preocupado por el presupuesto del Rally decide utilizar su helicóptero privado, pero haciendo un circuito de longitud mínima.
¿Cuál es la distancia mínima recorrida para hacer un circuito de longitud mínima? Explicar el circuito.
Las distancias en línea recta están indicadas en el siguiente cuadro:
| Andorra | Barcelona | Lugo | Tolouse | |
| Andorra | 0 | |||
| Barcelona | 140 | 0 | ||
| Luego | 730 | 800 | 0 | |
| Tolouse | 125 | 260 | 720 | 0 |
6.- Un problema de jardinero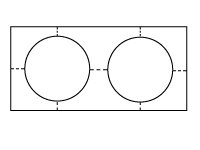
En una residencia, cinco vecinos quieren plantar en cada uno de sus jardines rectangulares de lado pequeño igual a 10 metros, dos árboles y flores, dispuestos tal como indica la figura adjunta.
Cada árbol está situado en el interior de un círculo y las flores fuera del mismo.
La distancia entre los dos círculos es igual a la distancia de cada círculo a los lados del rectángulo.
Preguntan a un jardinero, el cual, observando que los terrenos tienen el lado grande diferente , exclama: “No estoy seguro de poder hacerlo en todos!”
Dad vuestra opinión escribiendo SI o NO en cada casilla vacía del cuadro siguiente (en la hoja de respuestas)
|
Lado grande del jardín |
17m |
14m |
18’5m |
21m |
15m |
|
¿Es posible? |
7.- A la hora de los ángulo
¿Cuál es el valor exacto del ángulo formado por las agujas de un reloj cuando son las 10h 20′?
8.- En el horizonte
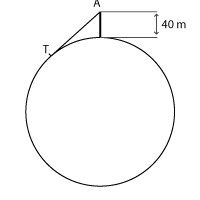
Desde el punto más alto A de un faro, situado a 40 metros sobre el nivel del mar se observa el horizonte.
¿A qué distancia de la punta del faro se encuentra aproximadamente el horizonte?
Indicación: Se trata de calcular al distancia AT (siendo T el punto de contacto de una tangente a la Tierra pasando por A). Como sabéis, la Tierra es redonda y la vuelta al mundo es de unos 40000 Km. (En el dibujo de aquí al lado, no se respetan, evidentemente, las proporciones)
Ernesto y yo hicimos los problemas 1, 2, 3 y 8, quizá bien, quizá mal. Una de nuestras complicaciones es que sólo teníamos como calculadora un móvil, y es bastante difícil hacer raíces de números con más de 10 dígitos… Pero acabo de comprobarlo, y quizá esté bien.
Un problemilla que hubo fue que no dio tiempo a hacer el sexto, por lo que acabamos poniendo Sí-No-Sí-No-Sí, y en el razonamiento “Porque conozco al jardinero”. En fin…
La verdad es que es algo muy entretenido, a lo que recomiendo ir. Si queréis apuntaros, visitad la web del TTM. La próxima sesión es el día 27 de este mes, a la que yo quiero ir ![]()
Una de las características del formato DIN-A es que las áreas de los distintos tamaños mantienen la proporción, es decir, que un DIN-A4 es el doble de grande que un DIN-A5, y la mitad de un DIN-A3. Esto es bastante útil por diversas razones, ya que un tamaño universal facilita mucho las cosas.
Si el año pasado yo no me podía creer que dos tercios de la clase hubiese suspendido el examen de Evaluación de Matemáticas, lo de ahora no tiene nombre: somos 30. Han suspendido 25. Cinco han aprobado. Un sexto de la clase. La media ya está por debajo del aprobado.
Bueno, si ellos son felices…
Por cierto, yo he sido uno de los que han aprobado, y he tenido la segunda nota más alta (8, frente al 8’5 del ganador). Lástima el haber perdido 0’25 por “chapucero” en un ejercicio…