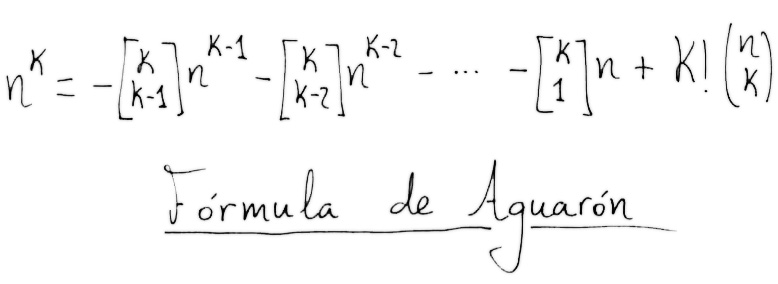Cosas en General

A una semana de la temida Selectividad todo alumno de 2º de Bachillerato que quiera dejar de serlo se empieza a poner nervioso ante la perspectiva de un buen concentrado de exámenes en apenas tres días. Y claro, como en todas las asignaturas entra todo el temario, toca repasar las tres evaluaciones. Lo cual es bastante pesado, pero en algunos casos te da una visión más general de la asignatura.

Hoy, sin ir más lejos, estábamos haciendo en clase de Física unos ejercicios de gravitación, lo típico para preparar el examen, cuando no sé cómo ha surgido el tema de que si las órbitas que describen los cuerpos celestes son elípticas no era lógico que en los problemas supusiésemos que son circulares. Ante eso, el profesor nos ha dicho que, efectivamente, se trata de una elipse, pero que el cálculo de esas trayectorias se eliminó del temario hace tiempo. Una ligera decepción para los que realmente teníamos curiosidad, pero nos ha comentado brevemente el tema y nos hemos quedado satisfechos. Sin embargo, un poco más tarde hemos pasado a la cuestión de los campos eléctricos y, como desde hace unos días ya sabemos integrar, hemos acabado hablando del Teorema de Gauss, que hace unos meses nos saltamos porque, por un lado, aún no sabíamos qué era una integral, y por otro, porque de nuevo es algo que no está en los planes de estudio. Y ni con esas, porque las herramientas matemáticas que son necesarias para trabajar con ese teorema ni siquiera aparecen mencionadas en el temario de 2º.

Contemplar cómo el nivel de asignaturas tan importantes para los futuros científicos o ingenieros como la Física y las Matemáticas no hace más que bajar es desolador. Y si al menos estuviesen ambos niveles compensados, pues no se notaría tanto la diferencia. Pero es que ya desde el curso pasado he necesitado conocimientos sobre cálculo diferencial e integral para poder comprender correctamente ciertos temas, y es bastante inconsecuente que esto se vea en un curso superior cuando hace poco más de 20 años se daba en 3º de BUP (el 1º de Bachillerato actual).

Quiero creer que la formación perdida durante los años de Educación Secundaria se acaba recuperando en la Universidad, pero personalmente preferiría que el puente por el que cruzo el Ebro estuviese diseñado por alguien que tenga una base técnica lo suficientemente sólida. Aunque si la respuesta oficial ante cualquier pregunta que se aleje del temario es “Es que eso no puedo explicároslo”, no sé yo si en unos años no haría mejor construyendo mi propia barca cuando quiera llegar a la otra orilla.

Como ya os comenté hace unas semanas, resulté seleccionado entre los ocho primeros de la fase aragonesa de la XLVIII Olimpiada Matemática Española. El pasado viernes 13 acudí con pompa y boato a la entrega de premios (el sitio lo merecía: el Patio de la Infanta, en la sede de Ibercaja. Por si no lo conocíais, tiene una historia muy interesante) dispuesto a pasar el ya clásico momento de nervios. En la sala estaban varios conocidos, la mayoría del TTM: profesores, alumnos, amigos…

Una vez estuvimos todos, las autoridades de rigor dieron sus respectivos discursos. Como siempre, cada uno barría hacia su casa:  más tarde, durante el aperitivo, me propusieron un par de responsables de la Universidad que hiciera Matemáticas o Física. Lo dicho, cuando todos los de traje hubieron hablado comenzó la parte interesante. La parte en la que se aceleró el pulso de 8 de los asistentes. Como ocurre en todas las entregas de premios, se va nombrando por orden de puntuación ascendente. En ese momento todos estábamos pendientes de las palabras de quien anunciaba los ganadores. Y, como siempre, estaba latente esa tensión por ver a quién nombraban el primero, ya que los siguientes son siempre mucho más fluidos; se podría decir que “salen solos”.

Pues bien, no me nombraron primero. Ni segundo, pero sí tercero: un honroso 6º puesto en la que será mi última Olimpiada Matemática, al menos a este nivel. He de admitir que al principio el resultado me decepcionó un poco, ya que tan sólo los tres primeros pasan a la fase nacional, y ésta se trataba de mi última oportunidad. Sin embargo, tras conocer las puntuaciones de los que representarán a Aragón en marzo no puedo sino admitir que ellos realmente lo merecían: al fin y al cabo, el 1º casi me duplicaba la puntuación. También era curioso que hasta el 4º puesto tuviésemos puntuaciones que no pasaban de los 22 puntos sobre 42, y ya el 3º tuviese 31 puntos. La brecha ha sido bastante considerable este año.

En cualquier caso, por muchas estadísticas y puntuaciones que pudiese analizar para intentar autoconsolorme, nada templó mejor los ánimos que el vino español que nos ofreció Ibercaja tras la ceremonia, y es que, al igual que el año pasado, salimos prácticamente comidos. Como yo ya repetía (el año pasado también fui seleccionado) estuve al tanto de los postres, y de nuevo logré acaparar gran parte de unos montaditos de chocolate y nata que hacen francamente bien.

También tengo que nombrar a Alberto Larrauri, que aun siendo de 4º de la ESO quedó 4º. Un logro realmente impresionante, teniendo en cuenta que la competición está orientada a alumnos de Bachillerato, y algunos de los problemas precisan de Matemáticas que se dan en 2º. Desde aquí, le doy mi enhorabuena

El viernes participé en la primera fase de la XLVIII edición de la Olimpiada Matemática Española. Al igual que el año pasado (cuando quedé 4º, a un par de puntos de clasificarme para la fase nacional), la prueba consistió en 6 problemas a resolver entre dos sesiones de tres horas y media de duración cada una.

La solución al primero, una progresión, era bien sencilla: 20n2. Pero, como siempre, existen dos caminos: el fácil y el difícil. Adivinad cuál elegí yo. Efectivamente, dicha progresión aritmética puede expresarse de forma sencilla (20n2), y de forma compleja, con números combinatorios y demás parafernalia. Pues bien, resulta que, accidentalmente, topé con la expresión compleja, pero no le di mayor utilidad que la de hacerme el interesante. Sin embargo, anteayer ordené los folios de borrador que empleé durante la Olimpiada, y encontré de nuevo la fórmula. La estuve examinando un rato, y me decidí a generalizarla. De ahí pasé a otra ecuación más general todavía, que, tras 38 carillas de sucio y unas 8 horas de quebraderos de cabeza evolucionó hasta la siguiente fórmula:

No sé si alguien la habrá encontrado antes, pero la alegría que experimenté al verla terminada no se puede describir con palabras. Quizá sólo con números [inserte risas enlatadas aquí].

En cuanto al resto de problemas, no hubo ninguna anécdota destacable. Tal vez que durante la sesión de la tarde no me encontraba del todo bien, y pasé unas dos últimas horas bastante malas, pero resistiéndome a rendirme aguanté como un Euler hasta el final. Acto seguido, me subí al despacho de Pepe a por un paracetamol; me lo había ganado.

Ésta fue la primera Olimpiada Matemática en la que participaba mi hermano, que aunque va a 4º de la ESO, gracias a un permiso especial de su profesor pudo participar entre los “mayores”. Y, la verdad, no le ha ido nada mal: ayer salieron los resultados, y está en el puesto 36 de la clasificación.

Aunque quisiera, yo no podría deciros el puesto en el que he quedado, ya que al estar ENTRE LOS 8 PRIMEROS no lo sabré hasta el día de la entrega de premios! En efecto, he vuelto a quedar en el top-8, pero hasta el día 13 de enero en el Patio de la Infanta no conoceré el resultado definitivo. No tengo muchas esperanzas, pero siempre cabe la posibilidad de que pueda pasar a la fase nacional…

Un par de días antes de que mis vacaciones en los Pirineos finalizaran, mi padre me explicó cómo resolver raíces cúbicas a mano empleando un curioso método que consiste en descomposición en sucesivas raíces cuadradas. Para que nos entendamos:

3√a = a^(1/3) = a^(4/12) = a^(1/12) * a^(3/12) = a^(1/12) * a^(1/4) = √(√(a)) * a^(1/12)

De este modo, y realizando el mismo procedimiento sucesivamente (en este caso, habría que volver a hacerlo con el elemento a^(1/12) ), nos iremos aproximando cada vez más y más al resultado real. Cuanto mayor sea el denominador de la potencia que no podemos calcular a mano, más se aproximará el valor del elemento a 1, y mejor será la estimación.

El código está basado en este principio, así como en una sucesión en la que reparé al realizar los cálculos a mano. En algún sitio hay un pequeño fallo que subsané sumando 2 a una variable, pero no tuve las ganas suficientes de rastrearlo a lo largo de las más de 10 carillas que rellené pensando en esto.

Y aquí está el código, yo lo he compilado empleando gcc en Ubuntu, pero para gustos, colores:

Como os comenté, durante estas dos últimas semanas he estado en Bilbao con la beca Campus Científicos de Verano. Desde el 17 hasta el 30 de julio he convivido con otras 29 personas con inquietudes científicas como yo, pero no era eso lo único que nos unía: a diferencia de lo que ocurre en otros campamentos o actividades organizadas para grupos, todos nosotros compartíamos carácteres y aficiones similares, lo que ha hecho que estos quince días hayan pasado volando. Mirando hacia atrás, me doy cuenta de las muchas cosas que he hecho a lo largo de estos días, pero curiosamente parecen menos por lo rápido que ha sucedido todo.

Cuando fui de viaje de estudios a Italia con el colegio me di cuenta de algo muy curioso, llamémoslo la regla del autobús: todo grupo lo suficientemente grande que haya de convivir durante un tiempo, acabará dividiéndose en un mínimo de dos grupos con diferencias sustanciales entre ellos. En el caso de Italia, esto era muy claro: en la parte de delante del autobús nos encontrábamos los frikis, y en la parte de detrás se hallaba la gente normal. Pues bien, si hubiese que meter a toda la gente de Euskampus en el mismo autobús que nos llevó a mi clase y a mí por toda la península itálica, al menos el 90% iría en la parte de delante. Quizá esta imagen lo explique mejor:

Pero bueno, como he dicho, esto se trata de un campus científico y, como tal, tenía algo de Ciencia. Bastante, de hecho: todos los días íbamos por la mañana a la Universidad del País Vasco a participar en los proyectos que nos habían sido asignados. La distribución era bastante sencilla: cada grupo de 7-8 personas tenía un proyecto para cada semana: Matemáticas, Física, Química o Biología. Los míos (¡sorpresa!) eran Física y Matemáticas, y en ambos proyectos estuve con las mismas personas.

El proyecto de la primera semana era el de Física, aunque era muy aplicado: lo que hicimos fue construir con nuestras propias manos dos generadores de Van de Graaff. Aunque tuvimos varios problemas que fuimos subsanando sobre la marcha,  el grande nos funcionó a la primera. El segundo, de menor tamaño, los terminamos a última hora, pero finalmente todo salió a la perfección. Además de aprender un montón acerca de la electricidad estática y este peculiar ingenio, también descubrimos varias formas de dar garrampazos a algún despistado que se hallase cerca y que meter tenedores metálicos en el microondas no es tan peligroso como parece.

Durante la segunda semana, más corta, nos dedicamos en cuerpo y alma a las Matemáticas, concretamente a la criptología y a la probabilidad. Creo recordar haber dicho que el ambiente de frikismo del grupo era considerable. Pues bien, los profesores de este proyecto eran dignos de ese ambiente. Creo que con eso se explican cosas como la siguiente:

La verdad es que, aunque no soy precisamente un acólito de la probabilidad, me gustó bastante el proyecto en conjunto: venía a ser una especie de selección de los mejores días del TTM.

El último día, el de la presentación en conjunto de los proyectos, tuvo su toque wtf cuando toda la sala (unos 30 estudiantes; 15 profesores; padres y visitantes; y peces gordos de la Uni) vio que nuestra última transparencia consistía en las letras de FIN (cada una de un color) cayendo lentamente sobre un fondo de arcoiris en .gif, y apareciendo un unicornio rosa (también en .gif) con la música de Mario Bros de fondo. Impresionante. Ese día también sorteamos los generadores Van de Graaff que habíamos construido, ¡y yo me llevé el grande! Y sí, mi madre dijo que o se va el Van de Graaff, o me voy yo.

Cuando no estábamos en la Uni también realizábamos actividades: fuimos al Guggenheim, a una gymkana matemática, a la playa, de excursión a un parque natural, a San Sebastián, a algún que otro museo…

En definitiva, una experiencia inolvidable. El único inconveniente es que ya no podemos repetir el año que viene, al ser una actividad únicamente disponible para alumnos de 4º de ESO y 1º de Bachillerato. Así que espero que el Ministerio recapacite acerca de su decisión, sabiendo que si no extiende la edad hasta 2º de Bachillerato todos nosotros estudiaremos Derecho.

Por cierto, durante la primera semana escribí junto con dos amigos un blog -obligado- acerca del campus llamado Not only mejillón Science. Puede que aún publique alguna cosa más sobre el campus en Cosas en General, pero ése está cerrado definitivamente.