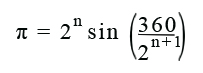Cosas en General

O, dicho de otra forma, cómo justifico no haber ganado (y mira que era fácil) en la prueba a la que me he presentado esta tarde, el Canguro Matemático.

Dejando de lado lo bueno que pueda ser cada uno resolviendo problemas de Matemáticas, un factor decisivo en este tipo de concursos (al igual que en otras muchas áreas) es la velocidad mental. Por ejemplo, a mí me cuesta bastante centrarme en cualquier problema, incluso si no es algo matemático. Por suerte, una vez he asimilado todos los datos, ya pienso en cómo resolverlo.

En la Olimpiada Matemática quedé en un puesto respetable porque no exige una gran rapidez, al contrario: 6 ejercicios, 7 horas. Eso da 1:10h para hacer cada problema. Eso sí, eran de gran complejidad (vamos, que no había por dónde agarrarlos: que tuviese completamente bien, yo sólo obtuve uno).

Sin embargo, este concurso del que he hablado, de mucho menor nivel (es para alumnos de ESO y Bachillerato, y se realiza en diversos Centros) busca exactamente lo contrario: se trata de 30 problemas cortos, de no mucha dificultad, divididos en tres categorías: fácil, medio y difícil. Pero claro, la dificultad está en el tiempo: hay sólo 1:15h para realizar todo el examen. Vamos, que para hacer 30 ejercicios de Canguro te dan el mismo tiempo que para uno olímpico.

Así que no espero llevarme nada, aunque quién sabe, siempre queda alguna posibilidad. Pero no, no creo: este concurso lo ganarán, cada uno en su respectiva categoría, mi hermano y Ernesto, que también lo hicieron (y ganaron) el año pasado.

Mi intuición se equivocaba. A pesar de haber hecho un examen bastante flojo, al parecer el jurado no lo vio tan mal, y he quedado 4º en la fase aragonesa de la XLVII Olimpiada Matemática. Realmente, no soy el cuarto, sino que estoy “justo después del 3º”, porque estamos tres personas con la misma puntuación.

Lo curioso es que salí del examen bastante desesperanzado, y mi padre me dijo que lo tenía todo mal (¡se equivocaba!), y además únicamente hice el día anterior algunos ejercicios. Así que el año que viene me lo prepararé, e intentaré pasar a la fase nacional. De todas maneras, tampoco me quejo: un aperitivo en el Patio de la Infanta y 100€ no son nada despreciables

Cuando ayer me llamaron no me lo podía creer. Salí de la prueba con ánimo de “se ha hecho lo que se ha podido, era muy difícil”, pero contra todo pronóstico ¡estoy entre los ocho primeros de Aragón!

El examen, que realizamos el pasado viernes 21, tuvo una duración de 7 horas, durante las cuales había que hacer lo que se pudiese con 6 problemas (aquí tenéis los enunciados, y en este otro sitio están ya resueltos) de nivel avanzado-imposible (yo fui incapaz de entender algunos). Lo cierto es que, perfecto, sólo creo tener uno, y el resto estarán a medias, si llega. Todavía no sé cuál ha sido mi puntuación, sólo que estoy entre los ocho primeros, y que el próximo viernes 11 nos comunicarán en un acto quiénes son los tres seleccionados (yo no estaré entre ellos, os lo aseguro) que pasarán a la Fase Nacional, que se celebrará en Pamplona entre los días 24 y 27 de marzo.

El único ejercicio anecdótico es el 2, que por necesitar de conocimientos de 2º de Bachillerato no supe hacer (como la mayoría). Avancé bastante, y lo dejé a medias, y como aún me quedaba un poco de tiempo para pasarlo a limpio, decidí comentarlo decentemente. Una chica del TTM me había dicho antes del examen que los correctores solían valorar los ejercicios originales, así que eso hice: lo comenté, pero en verso. Y así tenemos cosas como “¿Qué es, r, la razón? – Algo que dejamos para otra ocasión.”. O tambíen “Una incógnita hallaremos – Y al señor Pi llamaremos”. Probablemente me hayan seleccionado por mis dotes artísticas, más que matemáticas…

Y si conocéis a alguien que haya participado, aquí están las listas con los resultados, ordenadas por número o por puntuación.

Sí, habéis leído bien. Se puede hackear una calculadora. Aunque parezca increíble, es posible modificar el funcionamiento de varios modelos de Casio para añadir funciones ocultas, o se pueden mejorar las funciones de las calculadoras baratillas que todos tenemos. Tras un poquillo de investigación, he reunido una serie de hackeos o modificaciones que, además de ser útiles, sirven para fardar delante de los amigos. Mi intención original era condensarlos todos en una entrada, pero conforme he ido escribiendo, he descubierto más y más cosas acerca de la fascinante cara oculta de las calculadoras, así que lo repartiré a lo largo de algunos posts.

Esto tiene su base en un motivo muy sencillo: es más barato fabricar 2000 chips de tipo A que 1000 chips de tipo A y 1000 chips de tipo B. Tomemos el ejemplo de la fx-82ES y la fx-570ES. Por fuera tienen exactamente la misma forma:

fx-82ES - 15€

fx-570ES - 25€

La fx-82ES tiene unas 250 funciones, mientras que la 570ES unas 400. ¿Es mejor el circuito de ésta útlima? No, porque es el mismo. Una calculadora “baratilla” como la 82ES puede hacer lo mismo que una avanzada, como la 570ES. Lógicamente, la fx-82ES está capada, o tiene una ligera modificación, para que no muestre todas sus capacidades. Para conseguir ampliar las funciones de nuestra calculadora, hay que hacer unos pequeños cambios que varían en función del modelo. En la próxima entrada explicaré cómo actualizar dos modelos de calculadora (fx-82Es y fx-82MS) a las versiones “caras” (fx-570Es y fx-115MS, respectivamente). Más adelante, también comentaré algunos trucos y programas ocultos en las calculadoras Casio.

Se me ha ocurrido una forma de aproximarse a Pi bastante buena, y muy sencilla de entender.

Empecemos con un círculo, simplificado a 4 lados (l). De infinitos lados hemos pasado a 4, no está mal:

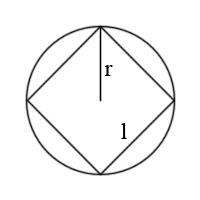
Si tomásemos ese cuadrado como un círculo, su longitud sería 4l. Supongamos que r vale 1 (además, así se simplifican los cálculos), por lo que l valdrá (Teorema de Pitágoras) . Si la fórmula de la longitud es 2(Pi)r, tendríamos que 4=2(Pi), por lo que Pi valdría 2.828…

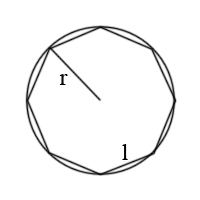
Ahora, tomemos un polígono de mayor número de lados (es más sencillo con los que tengan 2ⁿ lados). En este caso, 8.

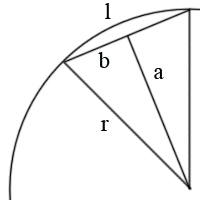
En este caso tenemos un triángulo isósceles cuyos lados iguales son r (1), y el desigual l. Para poder sacar el valor de l tenemos que partirlo por la mitad, de modo que tengamos dos triángulos rectángulos de lados r, a y b.
De este triángulo conocemos la hipotenusa (1), el ángulo recto y el que coincide con el centro de la circunferencia. Como la circunferencia mide 360º (simplificada en 2ⁿ lados, y nosotros tenemos la mitad del triángulo, ese ángulo será 2ⁿ⁺¹. Ahora que conocemos ese ángulo, podemos aplicar la fórmula del seno para hallar el valor de b. En este caso,

sin (360/16)=0.3827…

Como r=1, b=0.3827… Y como l=2b, l=0.7654… Por tanto, la longitud de esta circunferencia será 8l=6.1229…, y Pi tendrá un valor de 3.0615.

De todo esto se saca la siguiente fórmula:

Cuanto mayor sea el valor de n, más dígitos de Pi saldrán. Con n=21 salen 9 decimales. No es gran cosa, pero menos da una piedra.