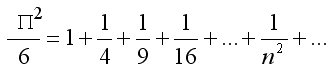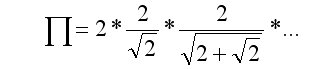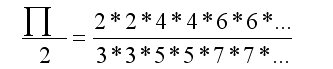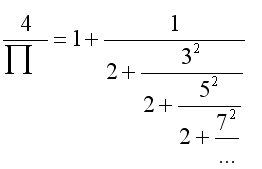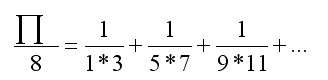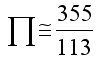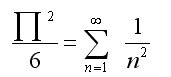ene
22
2009
¿Qué es el maná?
En la Biblia (Éxodo), aparece una escena en la que está el pueblo de Israel, precedido por Moisés, vagando por el desierto. Entonces encontraron unos árboles como este:
 Acamparon allí y, por la mañana, descubrieron que estaba todo de color blanco, y que eso era comestible. Además, a cada persona le sabía como su alimento favorito. Así que comieron en abundancia, saciando su estómago (y después, supongo, le dieron gracias a Yavé).
Acamparon allí y, por la mañana, descubrieron que estaba todo de color blanco, y que eso era comestible. Además, a cada persona le sabía como su alimento favorito. Así que comieron en abundancia, saciando su estómago (y después, supongo, le dieron gracias a Yavé).
Pero la explicación es más sencilla (y menos surrealista): por la noche, unos insectos comen durante varias horas la hojas de este árbol, y, claro, no se lo quedan todo para ellos. Los pobrecitos tienen que… evacuar.
Lo que se aprende en clase de Religión…
no comments | tags: curiosidad, razonamiento | posted in curiosidad
ene
21
2009

USB,
ropafriki.com
 “Los videojuegos han arruinado mi vida. Por suerte, aún me quedan dos vidas extra”, de TypeTees
“Los videojuegos han arruinado mi vida. Por suerte, aún me quedan dos vidas extra”, de TypeTees
 “No temo a la oscuridad”, brilla en la ídem. TypeTees
“No temo a la oscuridad”, brilla en la ídem. TypeTees

Ecualiseta. Para la que estoy ahorrando. En ThinkGeek.
 Y después de conseguir la ecualiseta, me compraré la Soundtrack T-shirt, que tiene altavoz y mando a distancia. Con ranura para SD. En ThinkGeek, cómo no.
Y después de conseguir la ecualiseta, me compraré la Soundtrack T-shirt, que tiene altavoz y mando a distancia. Con ranura para SD. En ThinkGeek, cómo no.
 En San Juan de Luz, Francia, el año pasado, vi una camiseta con esta foto. Debajo ponía “Legocentrique”. Lástima que no la encuentre por ninguna parte…
En San Juan de Luz, Francia, el año pasado, vi una camiseta con esta foto. Debajo ponía “Legocentrique”. Lástima que no la encuentre por ninguna parte…

Y esta ya no la venden, pero mola 
no comments | tags: curiosidad | posted in curiosidad
ene
11
2009

-”Y ahora, hermanos, oremos”
-”Espere, padre, que miro el correo”
no comments | tags: curiosidad | posted in curiosidad
dic
28
2008
Bastante curioso… Aparece en el libro que me estoy leyendo, “Biografía de la física”:
Cuando Hierón II llegó al poder, decidió donar una corona de oro a un templo en agradecimiento por los hechos venturosos; ordenó fabricarla a un orífice y le entregó el material necesario. El maestro cumplió el encargo para el día fijado. El rey estuvo muy satisfecho: la obra pesaba justamente lo mismo que el material que había sido entregado al orfebre. Pero poco tiempo después el soberano se enteró de que este último había robado cierta parte del oro sustituyéndolo con plata. Hierón montó en cólera y pidió a Arquímedes que inventara algún método para descubrir el engaño.
Pensando en este problema, el sabio fue a las termas y, una vez en la bañera, vio que se desbordó cierta cantidad de agua. Al descubrir de esa manera la causa del fenómeno, se lanzó a la calle, rebosante de alegría y en cueros, y corrió hasta su casa exclamando en alta voz: ‘¡Eureka!, ¡eureka!’.
Cuando llegó a su casa, Arquímedes tomo dos pedazos de oro y plata del mismo peso que la corona, uno de oro y otro de plata, llenó con agua un recipiente hasta los bordes y colocó en él el lingote de plata. Acto seguido lo sacó y echó en el recipiente la misma cantidad de agua que se desbordó, midiéndola previamente, hasta llenarlo. De esta manera determinó el peso del trozo de plata que correspondía a cierto volumen de agua. A continuación realizó la misma operación con el trozo de oro y, volviendo a añadir la cantidad de agua desbordada, concluyó que esta vez se derramó menos líquido en una cantidad equivalente a la diferencia de los volúmenes de los trozos de oro y plata de pesos iguales.
Después volvió a llenar el recipiente, colocó en él la corona y se dio cuenta de que se derramó una mayor cantidad de agua que al colocar el lingote de oro; partiendo de este exceso de líquido Arquímedes calculó el contenido de impurezas de plata, descubriendo de esa manera el engaño.
Vitrubio, S. I a.C.
no comments | tags: ciencia, curiosidad | posted in ciencia, curiosidad
dic
22
2008
Un décimo del gordo le ha tocado al pescatero al que siempre compra mi madre.
A alguien le tenía que pasar…
no comments | tags: curiosidad | posted in curiosidad
dic
16
2008
En el libro que me estoy leyendo, “El teorema del loro”, aparecen unas fórmulas con las que se obtiene el valor de pi. La verdad, me parece bastante curioso, aunque suponía que tenían que existir, ya que, hace 10 años, era difícil medir con precisión de decenas de decimales la longitud de un círculo…
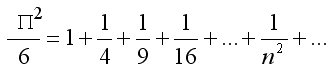
Leonhard Euler. Funciona.
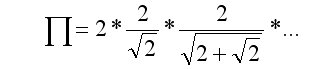 François Viète. Parece que el número que sale también se aproxima a pi.
François Viète. Parece que el número que sale también se aproxima a pi.
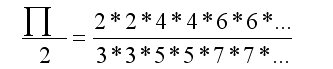 John Wallis. Si funciona, hay que poner muchos números (o me he equivocado).
John Wallis. Si funciona, hay que poner muchos números (o me he equivocado).
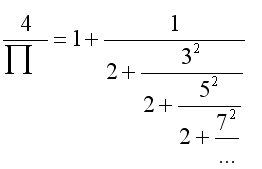 También de Euler. De momento, se me han quitado las ganas de resolverlo… De todos modos, si está en el libro, estará bien
También de Euler. De momento, se me han quitado las ganas de resolverlo… De todos modos, si está en el libro, estará bien 
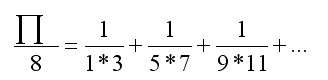 Gottfried W. Leibniz. Bastante más simple que las anteriores (me he atrevido a probarla, y parece que sale).
Gottfried W. Leibniz. Bastante más simple que las anteriores (me he atrevido a probarla, y parece que sale).
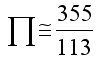 Y sin olvidar esta aproximación, bastante conocida, de Zhu Chongzhi (no tan conocido).
Y sin olvidar esta aproximación, bastante conocida, de Zhu Chongzhi (no tan conocido).
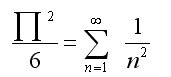 Simplificación de la primera de Euler.
Simplificación de la primera de Euler.
Por cierto, la imagen del principio
es mía.
no comments | tags: curiosidad, matemáticas | posted in curiosidad, matemáticas
 Acamparon allí y, por la mañana, descubrieron que estaba todo de color blanco, y que eso era comestible. Además, a cada persona le sabía como su alimento favorito. Así que comieron en abundancia, saciando su estómago (y después, supongo, le dieron gracias a Yavé).
Acamparon allí y, por la mañana, descubrieron que estaba todo de color blanco, y que eso era comestible. Además, a cada persona le sabía como su alimento favorito. Así que comieron en abundancia, saciando su estómago (y después, supongo, le dieron gracias a Yavé).